近日,我校數(shù)學(xué)與統(tǒng)計(jì)學(xué)院分析團(tuán)隊(duì)教師安慶楠與大連理工大學(xué)劉智超在C*-代數(shù)的分類問(wèn)題研究中取得重要突破。C*-代數(shù)的分類問(wèn)題又稱為Elliott猜想,其作為算子代數(shù)領(lǐng)域中的一個(gè)核心問(wèn)題,是由加拿大科學(xué)院院士George A. Elliott教授在1989年提出的。Elliott教授曾在1994年的蘇黎世國(guó)際數(shù)學(xué)家大會(huì)(ICM)上就該猜想做了45分鐘報(bào)告。(國(guó)際數(shù)學(xué)家大會(huì)由國(guó)際數(shù)學(xué)聯(lián)盟主辦,簡(jiǎn)稱ICM,是全球數(shù)學(xué)屆最高水平的學(xué)術(shù)會(huì)議,素有國(guó)際數(shù)學(xué)“奧運(yùn)會(huì)”之稱。首次會(huì)議于1897年在瑞士蘇黎世召開(kāi),已有100多年的歷史,一般4年一次。)
Elliott猜想主要分為兩部分內(nèi)容。第一部分:“Elliott單猜想”已經(jīng)得到了完全解決(可參見(jiàn)2018年和2022年ICM的45分鐘報(bào)告);而第二部分:“Elliott實(shí)秩零猜想”自上世紀(jì)90年代起,已近30年未曾有本質(zhì)性的突破。
Elliott實(shí)秩零猜想認(rèn)為完全K-理論(total K-theory) 是實(shí)秩零穩(wěn)定秩一C*-代數(shù)的完全不變量。我校教師安慶楠與大連理工大學(xué)劉智超在國(guó)際著名數(shù)學(xué)期刊《Proceedings of the London Mathematical Society》上發(fā)表了題為“Total Cuntz semigroup, extension, and Elliott Conjecture with real rank zero”的研究成果。(該期刊于1865年創(chuàng)刊,是倫敦?cái)?shù)學(xué)會(huì)的旗艦期刊,論文涵蓋廣泛的數(shù)學(xué)領(lǐng)域,致力于發(fā)表領(lǐng)域內(nèi)最高質(zhì)量和重要意義的文章。)兩人在該文章中使用擴(kuò)張理論的工具構(gòu)造了兩個(gè)實(shí)秩零穩(wěn)定秩一的C*-代數(shù),他們證明了這兩個(gè)代數(shù)具有相同的完全K-理論,但彼此之間并不同構(gòu)。這給出了Elliott實(shí)秩零猜想的反例。

此外,在這篇文章中,他們還對(duì)猜想的正則性條件進(jìn)行了修正,并使用完全K-理論給出了該修正下基于擴(kuò)張理論的分類定理;對(duì)于不滿足新正則性條件的一般情形,他們基于二人在分析學(xué)領(lǐng)域國(guó)際著名學(xué)術(shù)期刊《Journal of Functional Analysis》發(fā)表的題為“A total Cuntz semigroup for C*-algebras of stable rank one”的文章中構(gòu)造的完全Cuntz半群這一新的不變量工具分類了從一般擴(kuò)張中得到的反例代數(shù)。
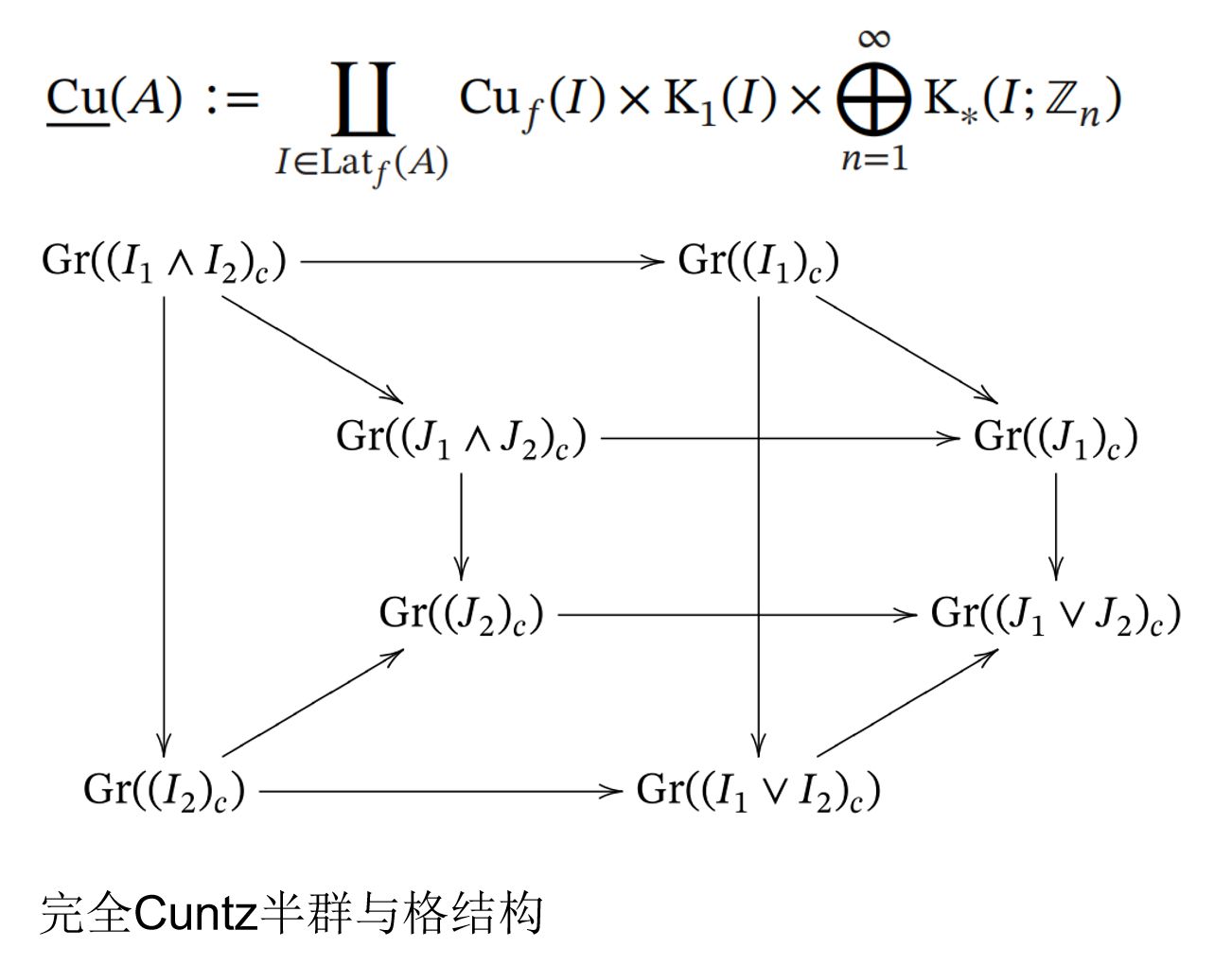
文章鏈接如下:https://doi.org/10.1112/plms.12595

安慶楠為我校數(shù)學(xué)與統(tǒng)計(jì)學(xué)院基礎(chǔ)數(shù)學(xué)學(xué)科分析團(tuán)隊(duì)講師,主要從事泛函分析方向的研究和教學(xué)工作,相關(guān)科研成果在《Proceedings of the London Mathematical Society》《Journal of Functional Analysis》《Journal of Operator Theory》《Science China-Mathematics》等期刊發(fā)表。2023年度,獲評(píng)天元東北中心優(yōu)秀青年學(xué)者。